Recursion means that “defining a haul in terms of itself“. In this post, you’ll learn to think recursively, and it could be a really powerful tool in writing algorithms.
The formula comes directly from Mathematics, wherever there are several samples of expressions written in terms of themselves
Best Courses to Learn Data Structures and Algorithm for cracking tech interview
Recursion is one most helpful method which might be utilized in rule design. So, understanding how recursion behaves in computer programs is obligatory for all computer engineers.
The formula isn’t hard, whereas thinking algorithmically may well be confusing in some cases.
The recursive algorithm has good blessings over identical unvarying algorithms corresponding to having fewer code lines and reduced use of information structures.
But, well-known drawbacks of recursion are high memory usage and the slow period since it uses a call stack.
Furthermore, every recursive resolution can be regenerate into even iterative solution victimization of the stack data structure, and vice versa.
How to Solve Recursion Problem?
Recursion is somewhat nuanced and very much depends on what downside you’re attempting to solve. However, there are some general steps we can return up thereupon can additional or less lead us in the right direction. Start your coding journey with Python, here’s how.
How to Think Recursively?
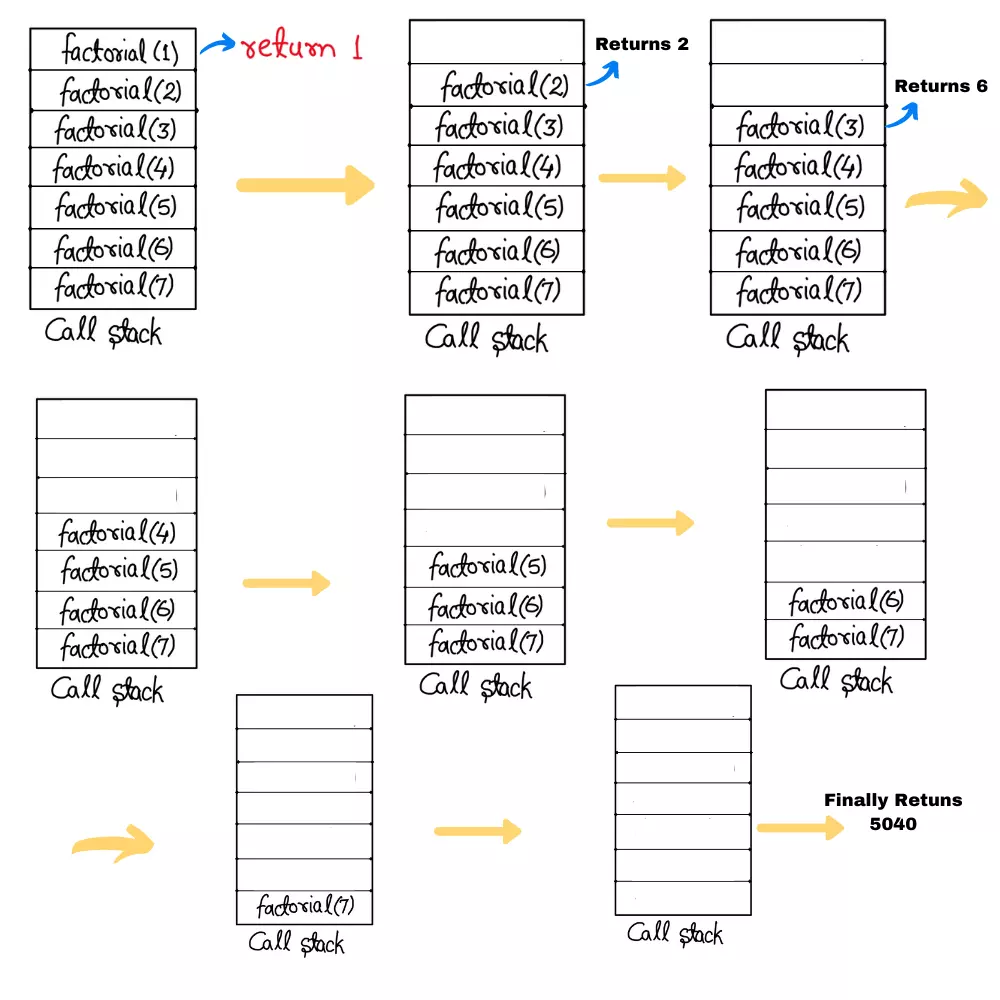
Here’s the recursion function for finding factorial of 7 using recursion. A big problem finds another subproblem and continues till it returns. Then the prior function gets the values of the caller function subsequently.

3 steps for recursion:
- Order Your Data
- Solve little Cases
- Solve Big Cases
Order Your Data
This step is completely the key to obtaining beginner in determination a drag recursively, and nonetheless, it’s often unmarked or performed implicitly.
Whether or not it is numbers, strings, lists, binary trees, or people, it is necessary to expressly notice an acceptable ordering that provides us a direction to maneuverer in to form the matter smaller.
This ordering depends entirely on the problem, however, an honest start is to consider the apparent orderings.
Numbers go together with their ordering, strings and lists are often ordered by their length, binary trees can be ordered by depth.
And other people are often ordered in an infinite range of smart ways. For example, height, weight or rank in an organization.
Once we’ve ordered our data, we can think of it as something that we can reduce. We can write out our ordering as a sequence:
0, 1, 2, …, n for integers
Solve Little Cases
This can be the unremarkably easiest part. Once we’ve got the proper ordering, we’d like to see at smallest components in our ordering and choose how we are progressing to handle them.
Once we have solved our base cases, and that we grasp our ordering, then finding the final case is simple.
Solve the Massive Case
Here, we tend to handle the information rightwards in our ordering, that is, data of a high degree.
Usually, we take into account data of arbitrary degree and aim to seek out how to unravel the matter by reducing it to an expression containing a similar problem of a lesser degree.
For example, in our Fibonacci example, we started with arbitrary n and reduced:
fib(n) to fib(n-1) + fib(n-2) that is an expression containing 2 instances of the problem we started with, of
lesser degree (n-1 and n-2, respectively).
There is often over one algorithmic case that we must think about as information of a given data type will take slightly different forms. However, it can entirely depend on drawback.
Memory for the function is divided into two parts one for stacking functional calls and other for memory heap that stores data to be referred and used by functions.
The call stack create a block for data and computation for each function that are not get returned and are arranged on top of each other and returned using FIFO principle
Should You Avoid Recursion?
There aren’t any definitive rules for once to and when to not use rule.
There are some times when recursion is necessary, and at different times, you have got to use your “programming instincts” to choose whether or not or not to solve recursively.
I know it may be frustrating, however like most style selections there’s no laborious rule.
The rule ought to be used once it is sensible to try and do so, and we avoid when it will not.
Any toughened engineer can acknowledge an algorithmic design immediately and have enough expertise to understand/debug it.
As a beginner, I will solely advocate that you simply experiment with each solution till you get compassionate when one is healthier than the other.
Recursion uses a lot of memory however is typically clearer and more readable. victimization loops will increase the performance, but the formula will sometimes be higher for the technologist.
Recursion in Python
When you call a function in Python, the interpreter creates a brand-new native namespace so names outlined among that function don’t impinge on identical names defined elsewhere. How to learn Python at an employable level?
# Python Program to find factorial of a +ve number
def recursive_factorial(num):
if num<0:
return "Sorry, factorial of negative numbers does not exist"
elif num == 1 or num == 0:
return 1
# recursive calls
return num*recursive_factorial(num - 1)
recursive_factorial(4) # returns 24One function will call another, and even though they each define objects with identical names, it all works out fine as a result of those objects exist in separate namespaces.
